{Tech Europe} x Open AI Hackathon (2025)
2nd place Team of 4 - Software using AI
Hello, I am Enzo, a student in data and artificial intelligence.
About me
I am currently pursuing a Master’s in Data and Artificial Intelligence at Institut
Polytechnique of Paris, eager to explore how technology can drive meaningful change.
I will be available for an internship starting in Mars 2026 to apply my knowledge and
skills in a practical setting. I'm also looking for PhD opportunities for September 2026.
Having always been enthusiastic about science, I am excited to explore how artificial
intelligence can solve complex challenges. What captivates me most about this
discipline is the opportunity to build tangible solutions. I enjoy blending creative
approaches with analytical thinking to develop innovative and practical results.
As I delve into new algorithmic techniques, I look forward to tackling increasingly
intriguing problems and contributing meaningfully to the ever-evolving landscape of
data and artificial intelligence.
Languages & Frameworks
Competitions
Hackathon by Zama, Hugging Face & Entrepreneur First (2024)
Participation Team of 3 - AI with Homomorphic Encryption
Hauts-de-France programming contest (2024)
3rd place Team of 3 - Algorithms & Mathematics
Code Game Jam (2024)
2nd place Large team - Game Development
Selected Projects
-
DL / Representation Learning
Discrepancies Detection Between Simulation and Reality Data
Analysing and quantifying the gap between coverage simulation and measurement data during my first-year Master’s internship.
-
Multi-model DL / Computer Vision
Deception Detection in video
Designing and implementing a multi-modal deep learning model to detect deception in video.
-
ML / LLM Waitlist
MagnOSS
Built a web application to teach chess, developed during the {Tech Europe} hackathon.
-
RL / DL
AI for Chess
Implemented chess engines with various reinforcement learning and deep learning techniques.
-
Simulation / Multi-agent Systems
Resilience of Economic Systems
Designed and implemented a complex simulation of worldwide economic systems to enable analysis.
-
NLP / SLM
Fine-tuning of SLMs for Summarization
Fine-tuned small language models for text summarisation tasks in another language.
-
DL / Time series analysis
Sub Tweet Event Detection
Developed a deep learning solution for detecting sub-tweet events.
-
Data Visualization / Statistics
Software for Football Analytics
Built a web application for visualising and analysing football match and player statistics.
-
ML / ACO
Ant Colony Optimization for Timetable Generation
Developed a web application to generate and manage school timetables using an Ant Colony Optimisation algorithm.
-
SQL / Software Engineering
Database Query Tool
Developed a web application enabling users to execute pre-defined SQL queries with custom options.
-
Software Engineering / Data Science
Software to Manage Quality Processes
Developed a web application to manage the industrial quality of petrochemical products.
-
Software Engineering
Toolboxes for development
Developed three toolboxes to support my projects: a frontend toolbox, a WebSocket toolbox, and a PyTorch toolbox.
-
RL / ML
AI for Connect 4 Game
Implemented various AI algorithms to play Connect 4 in C#, including reinforcement learning.
Experience
Master's degree in Data and Artificial Intelligence
Institut Polytechnique de Paris (Paris, France)
International program focused on Data Science, Machine Learning, and Artificial Intelligence.
Sept. 2024 - Aug. 206Bachelor's degree in Computer Science
Université Picardie Jules Verne (Amiens, France)
Application development track with two years of work-study program.
Courses completed: Mathematical Modeling, Decision Support, Advanced Programming,
Algorithmic Quality, Advanced Virtualization
High school diploma in Mathematics & Computer Science
Lycée Pierre Corneille (Rouen, France)
Graduated with Honors
Sept. 2018 - Aug. 2021Aviation Initiation Certificate
Lycée Pierre Corneille (Rouen, France)
Graduated with High Honors
Sept. 2020 - Oct. 2021Machine Learning Consultant for Mobile Networks
SFR Altice (Paris, France)
Continuation of internship mission (via Junior Enterprise) with a focus on enhancing and industrializing the deep learning solution for mobile radio coverage reconstruction, including integration into Google Cloud Platform.
November 2025 - August 2026Machine Learning Intern for Mobile Networks
SFR Altice (Paris, France)
Design and implementation of a deep learning solution that learns mobile radio coverage patterns and reconstructs theoretical coverage from real-world measurements.
April 2025 - August 2025IT Engineer Apprenticeship
Holdys - Petrochemical Industry (Yvetot, France)
Conceptualization and development of an application for managing quality processes
and optimizing delivery scheduling. Ensured user support, maintenance, and data
visualization.
Skills developed: software programming, agile methodology, data analysis,
autonomy, Python (Django framework) and SQL.
Web Developer
Luzaka - E-commerce (Malaunay, France)
I Developed custom modules for the Magento 2 CMS and redesigned the website's interface based on mockups. Deployed a new version of the CMS.
Summer 2022Logistics Assistant
Luzaka - E-commerce (Malaunay, France)
I assisted with unloading packages from trucks, organizing stock in designated areas (picking), and preparing orders for dispatch. Ensured efficient workflow and maintained a clean, organized workspace.
Summer 2021Contact
Let's get in touch
ACO
Timetable generation using ACO algorithm
As part of a team of four, we developed a web application for school
schedule management.
I designed the API using Django Framework and implemented
a schedule generator based on the Ant Colony Optimization algorithm.
The generator utilizes a scoring function to evaluate timetable quality,
drawing parallels to the dual problem in optimization.
This method enhances flexibility while adhering to critical constraints
regarding teacher and class availability.
The ACO algorithm explores solutions without pheromone expiration,
maintaining stability in the data. Additionally, a neighborhood
optimization function refines the results by testing promising
combinations after each iteration.
This approach aims to produce optimal timetables that enhance efficiency
and respect availability constraints.
fly over for more information
Score: 14%
{
SQLR
The Ant Colony Optimization algorithm is a metaheuristic algorithm inspired by the foraging behavior of ants.
It is used to solve combinatorial optimization problems.
The algorithm is based on the principle of pheromone deposition by ants on the ground.
The more ants pass through a path, the more pheromones are deposited on it.
This allows other ants to follow the path more easily.
The algorithm is based on the following principles:
- Construction of solutions
- Local search
- Updating of pheromones
The first step is to define a function to evaluate the quality of the solutions.
This function is named \( \text{score} \) and is defined as \( \text{score} : \mathbb{T} \to [0, 1] \)
where \( \mathbb{T} \) represents the set of all possible timetables.
The score function is expressed as a weighted sum (average) of various feature functions. Each feature function represents a specific characteristic of the timetable (\( \text{tt} \in \mathbb{T} \)):
\(
\:\text{score}(\text{tt}) = \sum_{i=1}^n \alpha_i \cdot f_i(\text{tt})
\)
| 08:00 | 08:30 | 09:00 | 09:30 | 10:00 | 10:30 | ... | 20:00 | |
|---|---|---|---|---|---|---|---|---|
| Monday | Course 1 | Course 2 | ... | |||||
| Tuesday | ... | |||||||
| ... | ... | |||||||
| Saturday | Course 3 | ... | ||||||
feature functions:
Number of hours for students
1. Penalty function for a day \( d \), based on the number of class hours \( h_d \):
\[
\text{penalty}(h_d) = \begin{cases}
1 & \text{if } h_d \leq 8 \\
e^{\text{-}k(h_d \, \text{-} \, 8)}& \text{if } h_d > 8, k \in \mathbb{T}^+
\end{cases}
\]
We chose \( k = 0.9 \) for this project.
2. Function \(\text{nb_hours_for_students}(tt)\), which uses this penalty for each day in the timetable (TT): \[ \text{nb_hours_for_students}(tt) = \sum_{d \in \text{tt}} \text{penalty}(h_d) / | \text{tt} | \] where \( h_d \) represents the total number of class hours on day \( d \).
Number of hours for teachers
2. Function \(\text{nb_hours_for_students}(tt)\), which uses this penalty for each day in the timetable (TT): \[ \text{nb_hours_for_students}(tt) = \sum_{d \in \text{tt}} \text{penalty}(h_d) / | \text{tt} | \] where \( h_d \) represents the total number of class hours on day \( d \).
1. Penalty function for a day \( d \) and a teacher \( d \), based on the number of class hours \( h_d \):
\[
\text{penalty}(h_{d, t}) = \begin{cases}
1 & \text{if } h_d \leq t.nb\_hours\_by\_day \\
0 & \text{if } h_d > t.nb\_hours\_by\_day
\end{cases}
\]
2. Function \(\text{nb_hours_for_teacher}(tt)\), which uses this penalty for each day in the timetable (TT)
and \(teachers_d\) the list of teachers for day \( d \): \[ \text{nb_hours_for_teacher}(tt) = \frac{1}{\left|\:\text{tt}\right|} * \sum_{d \in \text{tt}} \left( \frac{1}{\left|\:teachers_d \right|} * \sum_{t \in teachers_d} \text{penalty}(h_{d, t}) \right) \] where \( h_{d, t} \) represents the total number of class hours on day \( d \) for teacher \( t \).
Size of gaps between hours for students
and \(teachers_d\) the list of teachers for day \( d \): \[ \text{nb_hours_for_teacher}(tt) = \frac{1}{\left|\:\text{tt}\right|} * \sum_{d \in \text{tt}} \left( \frac{1}{\left|\:teachers_d \right|} * \sum_{t \in teachers_d} \text{penalty}(h_{d, t}) \right) \] where \( h_{d, t} \) represents the total number of class hours on day \( d \) for teacher \( t \).
1. Penalty function for a day \( d \), based on the number of gaps between class hours \( g_d \):
\[
\text{penalty_nb_gaps}(g_d) = e^{-\frac{g_d^2}{2 * \sigma^2}}
\]
Given that each time slot represents 30 minutes from 8:00 to 20:00, there are indeed 24 slots in a day. The maximum of possible gaps is 22 when there is a course at two extreme ends (8:00 and 20:00) and all other slots are empty. \( \sigma \in ]0, 22] \), we choose \( \sigma = 8 \)
2. Penalty function for a day \( d \), and a gap index \( i \) in the day \( d \), for exemple if the gap is between 8:30 and 9:00, the index is 1: \[ \text{penalty_gap_position}(g_{d, i}) = 1 - \frac{abs(i - midday)}{midday} \] where \( midday = \frac{nb\_slots}{2} = 12 \). The idear is to penalize gaps that are far from the middle of the day because they need less operations to be filled.
3. Function \(\text{nb_gaps_for_students}(tt)\), which uses these penalties for each day in the timetable (TT): \[ \text{nb_gaps_for_students}(tt) = \frac{1}{\left|\:\text{tt}\right|} * \sum_{d \in \text{tt}} \left( \beta_1 * \text{penalty_nb_gaps}(g_d) + \frac{\beta_2}{\left|\,g_d\right|} * \sum_{i}^{g_d} \text{penalty_gap_position}(g_{d, i}) \right) \] In this function, \( \beta_1 \) and \( \beta_2 \) are hyperparameters that we set to 0.75 and 0.25 respectively.
Size of gaps between hours for teachers
2. Penalty function for a day \( d \), and a gap index \( i \) in the day \( d \), for exemple if the gap is between 8:30 and 9:00, the index is 1: \[ \text{penalty_gap_position}(g_{d, i}) = 1 - \frac{abs(i - midday)}{midday} \] where \( midday = \frac{nb\_slots}{2} = 12 \). The idear is to penalize gaps that are far from the middle of the day because they need less operations to be filled.
3. Function \(\text{nb_gaps_for_students}(tt)\), which uses these penalties for each day in the timetable (TT): \[ \text{nb_gaps_for_students}(tt) = \frac{1}{\left|\:\text{tt}\right|} * \sum_{d \in \text{tt}} \left( \beta_1 * \text{penalty_nb_gaps}(g_d) + \frac{\beta_2}{\left|\,g_d\right|} * \sum_{i}^{g_d} \text{penalty_gap_position}(g_{d, i}) \right) \] In this function, \( \beta_1 \) and \( \beta_2 \) are hyperparameters that we set to 0.75 and 0.25 respectively.
1. Penalty function for a day \( d \), based on the number of gaps between class hours \( g_d \):
\[
\text{penalty_nb_gaps}(g_d) = e^{-\frac{g_d^2}{2 * \sigma^2}}
\]
Given that each time slot represents 30 minutes from 8:00 to 20:00, there are indeed 24 slots in a day, with up to 22 gaps possible if a class is placed at only two extreme ends (8:00 and 20:00) and all other slots are empty. \( \sigma \in ]0, 22] \), we choose \( \sigma = 8 \)
3. Function \(\text{nb_gaps_for_students}(tt)\), which uses these penalties for each day in the timetable (TT): \[ \text{nb_gaps_for_students}(tt) = \frac{1}{\left|\:\text{tt}\right|} * \sum_{d \in \text{tt}} \text{penalty_nb_gaps}(g_d) \]
Number of hours on Saturday
3. Function \(\text{nb_gaps_for_students}(tt)\), which uses these penalties for each day in the timetable (TT): \[ \text{nb_gaps_for_students}(tt) = \frac{1}{\left|\:\text{tt}\right|} * \sum_{d \in \text{tt}} \text{penalty_nb_gaps}(g_d) \]
1. Penalty function for saturday \( d \), based on the number of slots (half hours) \( h_d \):
\[
\text{penalty_saturday_hours}(g_d) = e^{-0.3 * h_d}
\]
I've chosen 0.3 as a hyperparameter to penalize fast the number of hours on saturday.
Size of the lunch break
1. Penalty function for a day \( d \), based on the number of slots (half hours) free between 11:30 and 13:30 \( h_d \):
\[
\text{penalty_lunch_break}(g_d) = \frac{1}{e^{-5(h_d - 0.9) + 1}}
\]
I used a sigmoid function to penalize if the lunch break is smaller than an hour. The hyperparameter are adjusted to fit the problem.
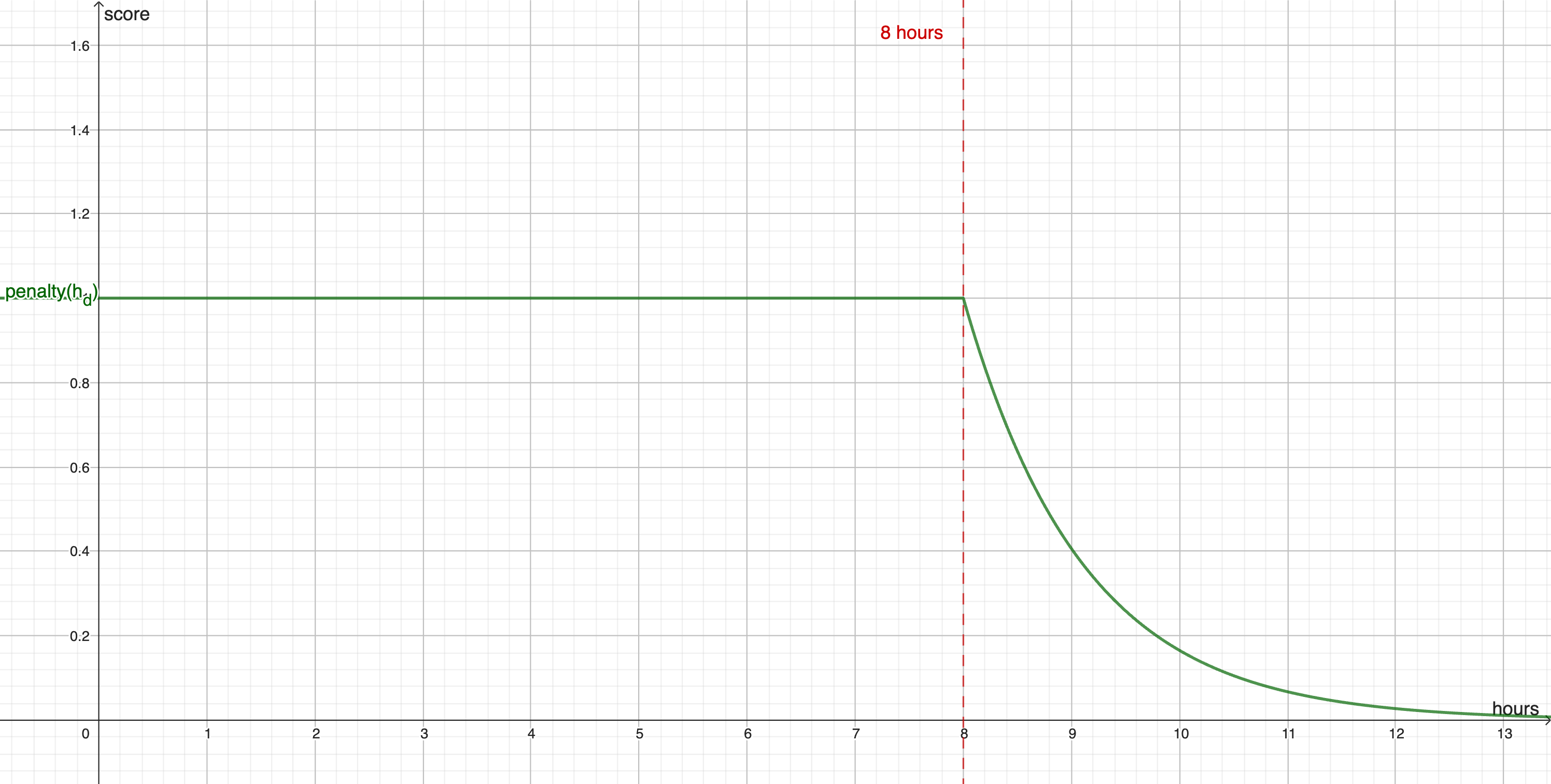
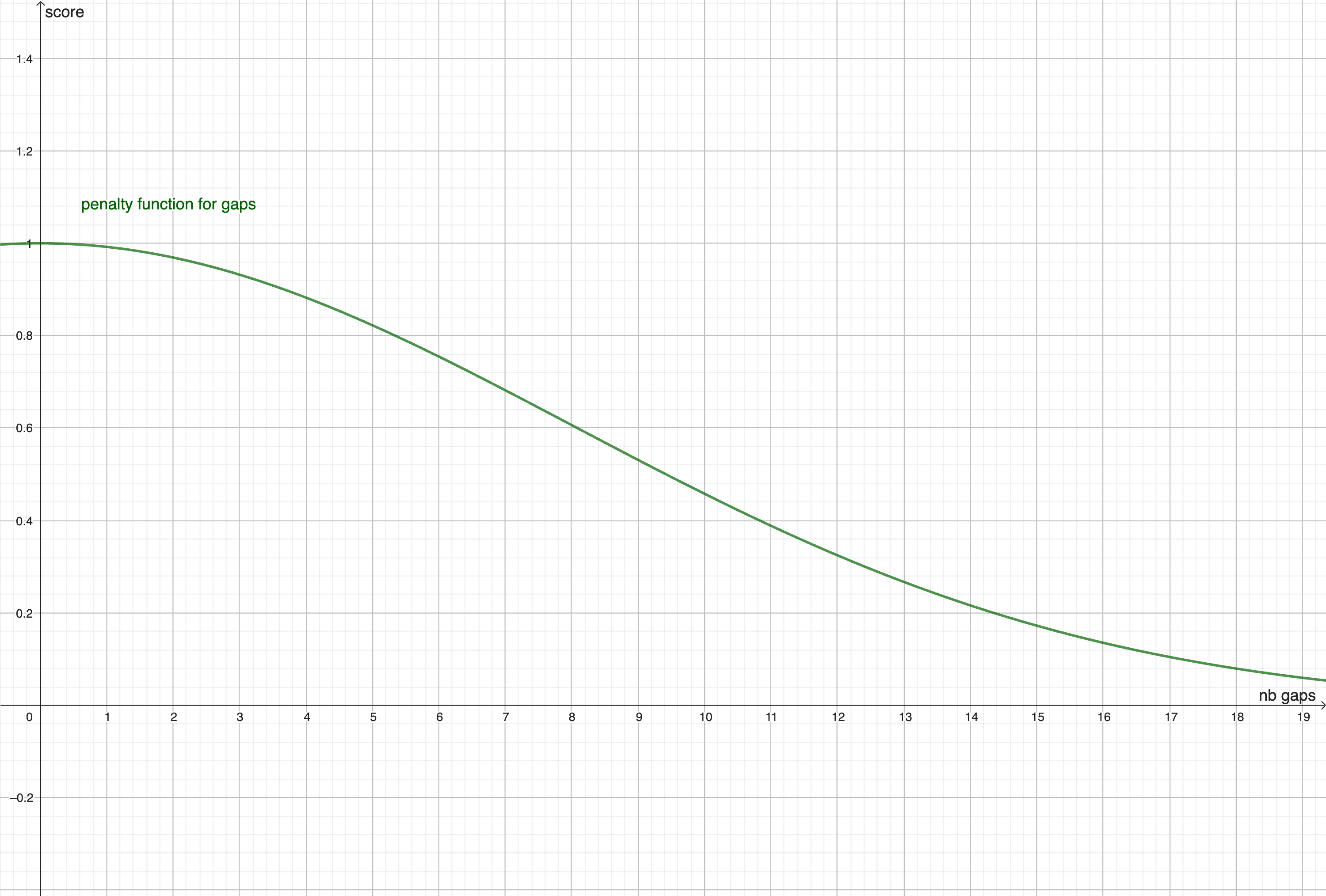
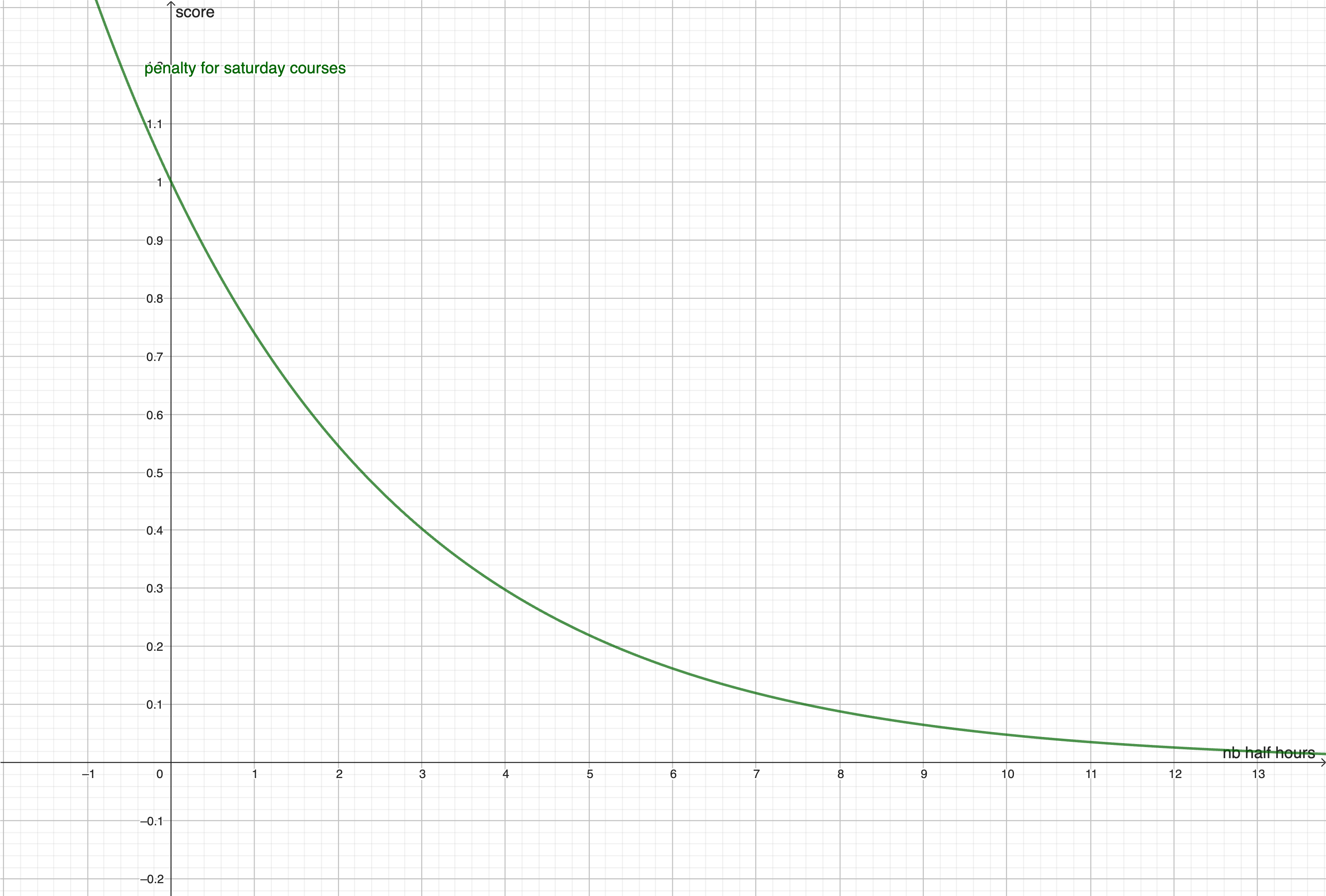
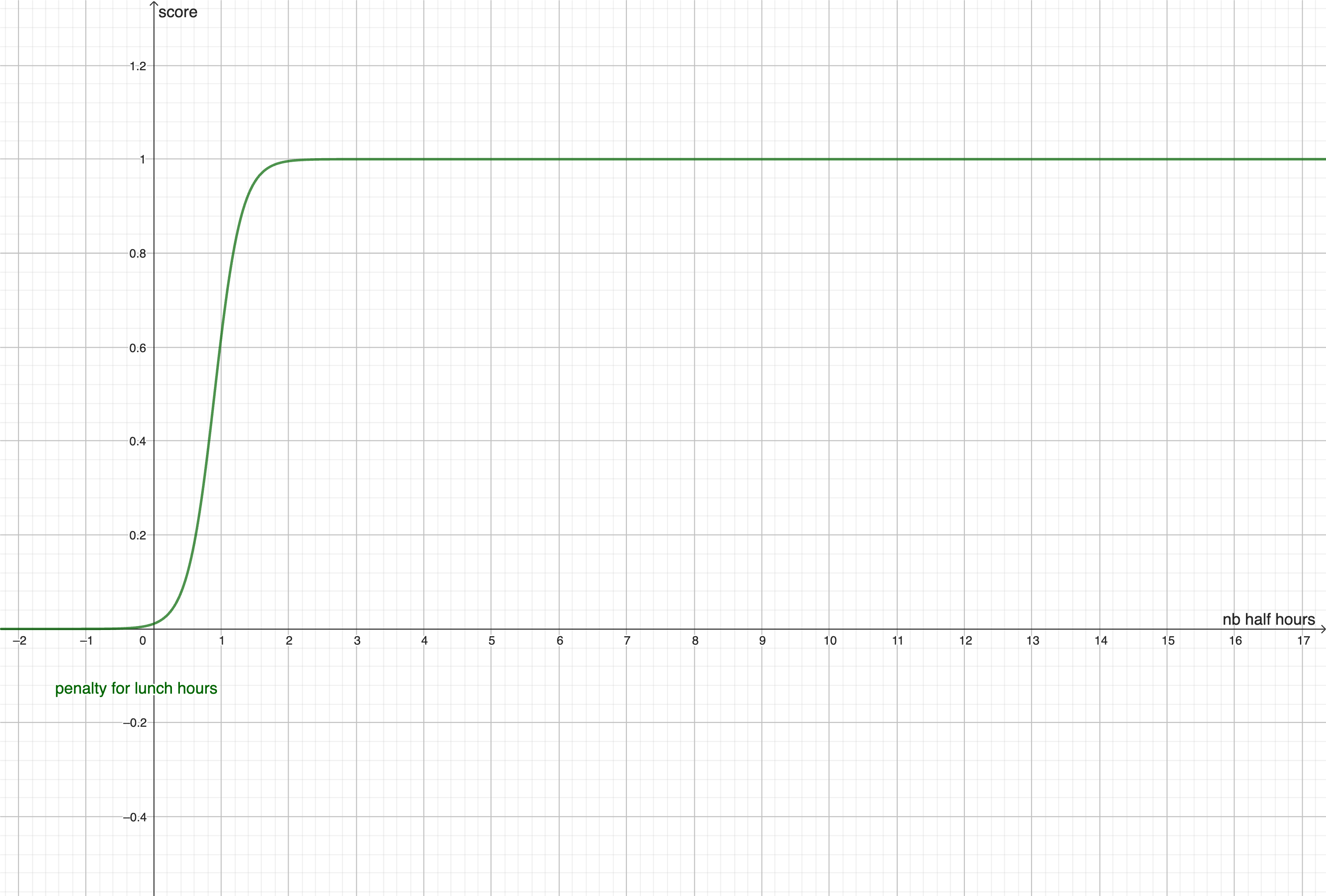
We consider \( \Omega \) as the set of all possible association of (day, hour of beginning, course) for a week.
If we consider \( \text{tt} \in \mathbb{T}_{week} \) and \(\Omega_{tt} = \bigcup_{d \in \text{tt}, h \in \text{tt}_d} \{d, h, tt_{d,h}\} \), then \(\Omega_{tt} \subseteq \Omega\).
It follow that the score function is also applicable to the subset \(\Omega_{tt}\): \( score(tt) = score(\Omega_{tt}) \)
\(\Omega_{i} = \{\alpha_1, \alpha_2, ..., \alpha_n\}\) with \(\alpha_i \in \Omega\)
We define \( P_i \) the probability to choose \( \alpha_i \) and \( \Omega^{\displaystyle \prime} \) the association between know score and \(\alpha_i\) (also named the learning/pheromone table).
In fact, every time we generate a timetable we had the score associated with every \( \alpha_i \) in \( \Omega^{\displaystyle \prime} \).
\[
P_i = \gamma * impact + \varepsilon * \Omega^{\displaystyle \prime}_i
\]
where \( \gamma \) and \( \varepsilon \) are hyperparameters, \( \Omega^{\displaystyle \prime}_i \) is the average score associated with \(\alpha_i\).
\(\varepsilon = 1 - \gamma\) we start the algorithm with \( \gamma = 1 \) and \(\Omega^{\displaystyle \prime}_i = \{\} \). After each iteration, we incrase \( \varepsilon \).
The impact function is determinist and represents how many other \(\alpha \) will be not available if we choose \(\alpha_i\). For exemple if we choose a course on monday at 8:00, we can't choose another course at 8:00 on monday, so we will impact all the other association on monday at 8:00 as well as the association with the same course. The impact is considered more important if an impacted association don't has a lot of other possibilities.
The \(\alpha_i\) selected is the result of a random choice based on the probability distribution \( P \).
As illustration, we will place a new course (Course 4) of 1 hour in the timetable.
Step 1: Find the available slots for the course
To simplify the calculation, we will limite the availables slots to 3, we will consider other slots as not available due to the availability of the teachers (for exemple).
| 08:00 | 08:30 | 09:00 | 09:30 | 10:00 | 10:30 | ... | 20:00 | |
|---|---|---|---|---|---|---|---|---|
| Monday | Course 1 | Course 2 | ... | |||||
| Tuesday | ... | |||||||
| ... | ... | |||||||
| Saturday | Course 3 | ... | ||||||
We will define \( \gamma = 0.1 \) and \( \varepsilon = 0.9 \) for this example.
The information about the Course 4 in \(\Omega^{\displaystyle \prime}\) are:
\(\{Monday, 9:00, Course 4\} \rightarrow 0.7\)
\(\{Tuesday, 09:30, Course 4\} \rightarrow 0.55\)
\(\{Saturday, 10:00, Course 4\} \rightarrow 0.2\)
Because there is no other courses to place, the impact function return 1 for each association.
Step 2: calculate the probability distribution
\[
P = \begin{cases}
0.1 * 1 + 0.9 * 0.7 = 0.73 & \text{if we choose Monday, 9:00} \\
0.1 * 1 + 0.9 * 0.55 = 0.595 & \text{if we choose Tuesday, 09:30} \\
0.1 * 1 + 0.9 * 0.2 = 0.28 & \text{if we choose Saturday, 10:00} \\
\end{cases}
\]
\[
P = \begin{cases}
0.1 * 1 + 0.9 * 0.7 = 0.73 \\
0.1 * 1 + 0.9 * 0.55 = 0.595 \\
0.1 * 1 + 0.9 * 0.2 = 0.28 \\
\end{cases}
\]
Finally, we do a random choice based on the probability distribution \( P \), in this case, it's most likely that the course will be placed on Monday at 9:00.
The final step (when all the courses are set) is to execute the neighborhood optimization function to refine the timetable. In this project i created a function that can be executed in \( O(n) \) where \( n \) is the number of placed courses in the worst case.
SQL Request
During my work-study program, I developed SQLR, a powerful SQL query management tool, to improve data accessibility and usability.
The tool was designed using Django and supports MySQL and SQL Server databases. SQLR introduces a file explorer for query organization and a streamlined query builder, simplifying SQL syntax management. Additionally, SQLR supports variable creation and API integration, enabling dynamic, multi-source data queries.
This tool allows users to manage efficiently complex queries and enhances data accessibility with an intuitive interface. SQLR abstracts the database language after connection, providing an unified interface for both MySQL and SQL Server users.
Finally, SQLR offers a comprehensive and optimized solution for data management and query execution.
More information
SQLR is a web application that allows users to execute SQL queries on a MySQL or SQL Server database. The software is build in two layers, the first one is used to save the generic queries as well as the database connection information. The second layer is the query builder that translates the user's query into a SQL query.
SQLR offers the possibility to use variables, editabled by the user before the execution of the query. The software is by default protected against SQL injection and other security issues, however, during the creation of a request, the user can specify to inject a variable in order to create dynamic queries or for other reasons. When a variable is injected, a function is called to check the content of the variable and to prevent any security issue.
The user can also create python functions that will be executed before the query to prepare the variables, for exemple to format a date or to lowercase etc.
The most advanced functionnality is the imbrication of queries (using CTE). In fact, the user can create a CTE from an other SQLR query. This allows to create complex queries and to use the result of a query in an other one. If a query in a CTE has variables, the user can map the variables of the CTE to the variables of the main query or give them a default value.
The query imbrication is managed by a tree, there is no limit of imbrication. The tree allows the software to optimize the imbrications and to execute the queries in the right order.
In this exemple we will consider a query Z that uses the result of the queries B, C and D. These queries use the result of the query A.
Query Z has two parameters,
Queries A, B, C and D have one parameter.
The following schema represents the tree of the imbrication.
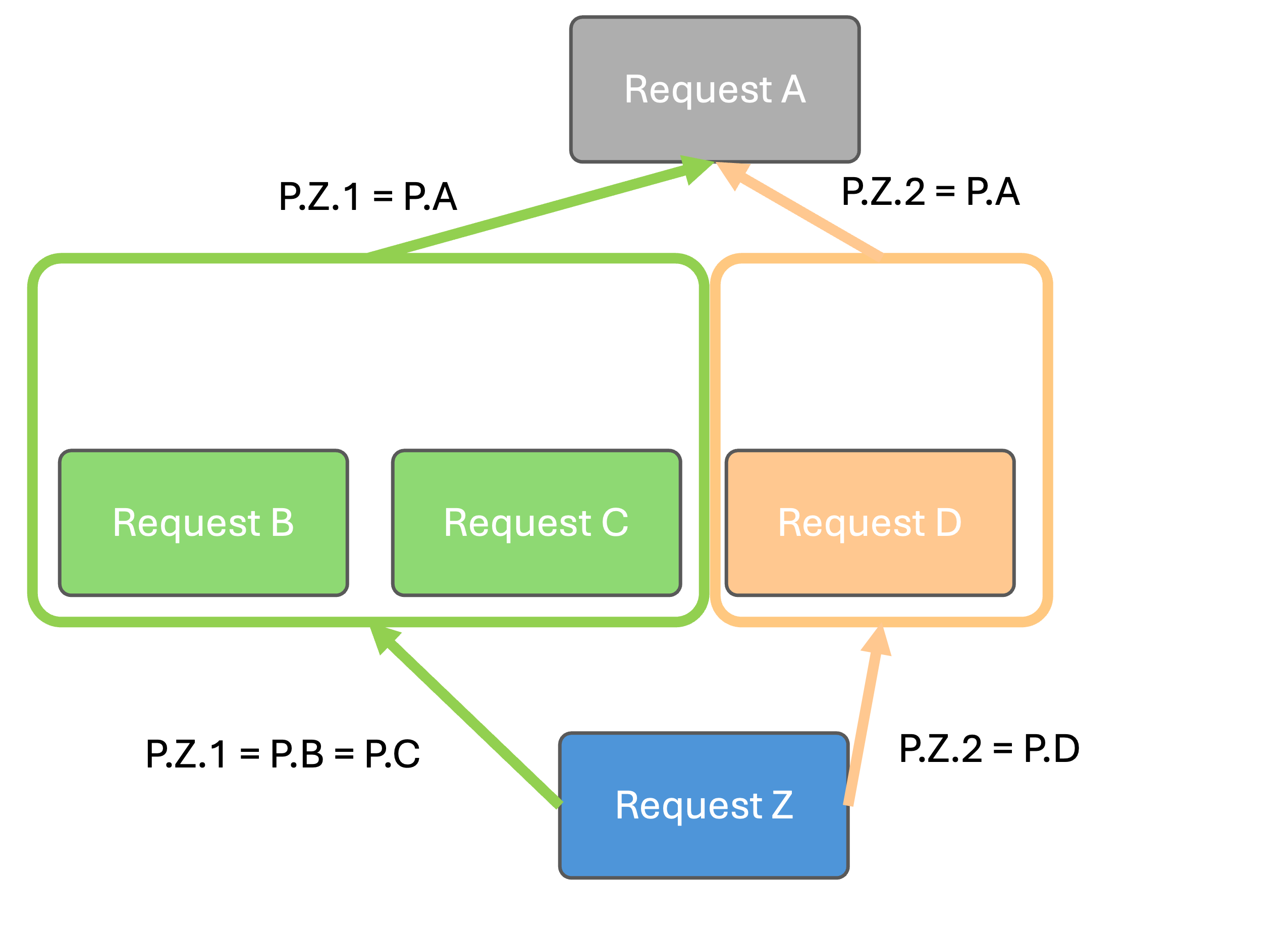
The tree is used to optimize the imbrication of the queries. In this case, the query A will be executed first, in two different variations, the first one with the parameter P.Z.1 and the second one with the parameter P.Z.2.
Connect 4
The grid in this Connect 4 implementation is vectorized, allowing for efficient updates by recalculating only neighboring vectors as tokens are added. This approach enables rapid win-condition verification, requiring checks on a small subset of vectors rather than a full grid scan.
This vector-based structure also strengthens the AI algorithms:
- The first bot employs a basic greedy algorithm, functioning as an "easy" level opponent.
- The second bot uses a Monte Carlo method to explore possible moves.
- The third bot leverages an advanced Monte Carlo approach with a projection system that identifies high-priority cells, focusing on strategically important moves.
The project is fully developed in C#.